一、sin无穷等于多少
sin无穷等于sinx,正弦(sine)是数学术语,在直角三角形中,任意一锐角∠A的对边与斜边的比叫做∠A的正弦,记作sinA(由英语sine一词简写得来),即sinA=∠A的对边/斜边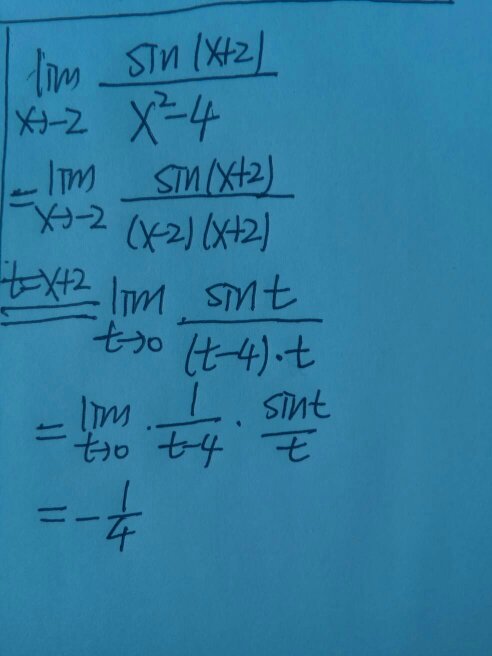
三角函数是数学中属于初等函数中的超越函数的一类函数。它们的本质是任意角的集合与一个比值的集合的变量之间的映射。通常的三角函数是在平面直角坐标系中定义的,其定义域为整个实数域。另一种定义是在直角三角形中,但并不完全。
二、sin正无穷极限等于多少?
sinx趋近于无穷大的极限是0。
极限为0,因为当x趋近于无穷大的时候sinx的取值范围是【-1,1】。而x为分母,当趋近于无穷大的时候sinx/x的极限是0,若数列的极限存在,则极限值是唯一的,且它的任何子列的极限与原数列的相等。
极限的性质:
和实数运算的相容性,譬如:如果两个数列{xn} ,{yn} 都收敛,那么数列{xn+yn}也收敛,而且它的极限等于{xn} 的极限和{yn} 的极限的和。
sin无穷大等于接近1。因为直角三角形的直角边总小于斜边。sin无穷大的极限不存在,即当x趋于无穷大时sinx的极限不存在。这是因为当x=k兀趋于无穷大时sinx恒等于零,当x=(2k+1/2)兀趋于无穷大时sinx恒等于1,它们不相等。
三、sin无穷等于多少?
sin(无穷)并无实际意义,sin函数的值在-1和+1之间变化。
sin函数为周期函数,在一定的周期内(2π)sin函数的值在-1和+1之间变化。所以不乱函数的取值是多少,其值总是在-1和+1之间,无法进行计算。
扩展资料:
倍角半角公式:
sin ( 2α ) = 2sinα · cosα 。
sin ( 3α ) = 3sinα - 4sin & sup3 ; ( α ) = 4sinα · sin ( 60 + α ) sin ( 60 - α )。
sin ( α / 2 ) = ± √( ( 1 - cosα ) / 2)。
三角函数简介:
三角函数是数学中属于初等函数中的超越函数的一类函数。它们的本质是任意角的集合与一个比值的集合的变量之间的映射。通常的三角函数是在平面直角坐标系中定义的,其定义域为整个实数域。另一种定义是在直角三角形中,但并不完全。
四、sin无穷等于多少?
sin(无穷)并无实际意义,sin函数的值在-1和+1之间变化。
sin函数为周期函数,在一定的周期内(2π)sin函数的值在-1和+1之间变化。所以不乱函数的取值是多少,其值总是在-1和+1之间,无法进行计算。
扩展资料:
倍角半角公式:
sin ( 2α ) = 2sinα · cosα
sin ( 3α ) = 3sinα - 4sin & sup3 ; ( α ) = 4sinα · sin ( 60 + α ) sin ( 60 - α )
sin ( α / 2 ) = ± √( ( 1 - cosα ) / 2)
由泰勒级数得出:sinx = [ e ^ ( ix ) - e ^ ( - ix ) ] / ( 2i )
级数展开:sin x = x - x3 / 3! + x5 / 5! - ... ( - 1 ) k - 1 * x 2 k - 1 / ( 2k - 1 ) ! + ... ( - ∞ < x < ∞ )
五、sin∞为多少呀?
数形结合,可以清晰的回答您的问题。
供参考,请笑纳。