一、圆的割线的定义是什么？
在直线和圆的位置关系中：直线和圆有两个公共点，我们说这条直线和圆相交，这条直线叫做圆的割线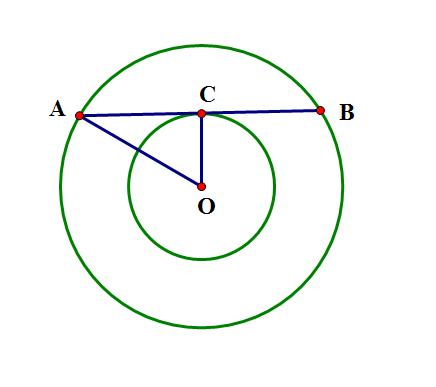
区别于圆的切线：直线和圆只有一个公共点，这时我们说这条直线和圆相切，这条直线叫做圆的切线。
希望可以帮到你。
二、割线与切线的关系是什么?
切线是一种特殊的割线，切线就是相切，割线就是相交。切线与那个图形只有1个交点，而割线有2个。
一条直线和圆如果只有一个交点就叫切线，一条直线和圆如果有两个交点就叫割线。
几何上，切线指的是一条刚好触碰到曲线上某一点的直线，更准确的说，当切线经过曲线上的某点（即切点）时，切线的方向与曲线上该点的方向是相同的，此时，“切线在切点附近的部分”最接近“曲线在切点附近的部分”（无限逼近思想）。
切割线定理：
从圆外一点引圆的切线和割线，切线长是这点到割线与圆交点的两条线段长的比例中项，与圆相交的直线是圆的割线。
切割线定理揭示了从圆外一点引圆的切线和割线时，切线与割线之间的关系。这是一个重要的定理，在解题中经常用到。
推论：从圆外一点引圆的两条割线，这一点到每条割线与圆的交点的两条线段长的积相等。
三、请问，什么叫圆的切线和割线？还有正弦和余弦是什么呢？
圆的切线:与圆只有一个公共点的直线。
圆的割线:与圆有两个公共点的直线。
正弦：
在直角三角形中，任意一锐角∠A的对边与斜边的比叫做∠A的正弦，记作sinA，即sinA=角A的对边/斜边
余弦：
在直角三角形中，任意一锐角∠A的邻边与斜边的比叫做∠A的余弦，记作cosA，即cosA=角A的邻边/斜边
四、圆的切线的定义是什么？
圆的切线是指一直线若与一圆有交点，且只有一个交点，那么这条直线就是圆的切线。几何上，切线指的是一条刚好触碰到曲线上某一点的直线。P和Q是曲线C上邻近的两点，P是定点，当Q点沿着曲线C无限地接近P点时，割线PQ的极限位置PT存在且唯一，则PT叫做曲线C在点P的切线，P点叫做切点；经过切点P并且垂直于切线PT的直线PN叫做曲线C在点P的法线。
平面几何中，将和圆只有一个公共交点的直线叫做圆的切线．这种定义不适用于一般的曲线；PT是曲线C在点P的切线，但它和曲线C还有另外一个交点；相反，直线l尽管和曲线C只有一个交点，但它却不是曲线C的切线。
五、切线的定义是什么？
几何上切线指的是一条刚好触碰到曲线上某一点的直线。
当切线经过曲线上的某点（即切点）时，切线的方向与曲线上该点的方向是相同的。平面几何中，将和圆只有一个公共交点的直线叫做圆的切线。
扩展资料：
切线主要性质
（1）切线和圆只有一个公共点；
（2）切线和圆心的距离等于圆的半径；
（3）切线垂直于经过切点的半径；
（4）经过圆心垂直于切线的直线必过切点；
（5）经过切点垂直于切线的直线必过圆心；
（6）从圆外一点引圆的切线和割线，切线长是这点到割线与圆交点的两条线段长的比例中项。
