一、三角形物体质心怎么求?
三边中线的交点,即三个顶点与对边中点的连线的交点,两个结果一样
三角形ABC,E、F是AB,AC的中点。EC、FB交于G。
证明:过E作EH平行BF。
∵AE=BE且EH//BF
∴AH=HF=1/2AF(中位线定理)
又∵ AF=CF
∴HF=1/2CF
∴EG=1/2CG(⊿CFG∽⊿CHE)
扩展资料:
质点系的质心仅与各质点的质量大小和分布的相对位置有关。
当物体具有连续分布的质量时,质心C的矢径 rc=∫ρrdτ/∫ρdτ,式中ρ为体(或面、线)密度;dτ为相当于ρ的体(或面 、线)元 ;积分在具有分布密度ρ的整个物质体(或面、线)上进行。
由牛顿运动定律或质点系的动量定理,可推导出质心运动定理:质心的运动和一个位于质心的质点的运动相同,该质点的质量等于质点系的总质量,而该质点上的作用力则等于作用于质点系上的所有外力平移 到这一点后的矢量和 。
参考资料来源:百度百科-质心
二、求几何图形重心、形心、质心的公式,分别是什么?
计算公式是∫∫Dxdxdy=重心横坐标×D的面积。
形心计算公式是∫∫Dxdxdy=重心横坐标×D的面积,∫∫Dydxdy=重心纵坐标×D的面积。形心就是截面图形的几何中心,质心是针对实物体而言的,而形心是针对抽象几何体而言的,对于密度均匀的实物体,质心和形心重合。
性质
一个凸对象的几何中心总在其内部。一个非凸对象的几何中心可能在外部,比如一个环或碗的几何中心不在内部。
三角形的重心与三顶点连线,所形成的六个三角形面积相等,顶点到重心的距离是中线的。
重心、外心、垂心、九点圆圆心四点共线。重心、内心、奈格尔点、类似重心四点共线。三角形的重心同时也是中点三角形的重心。形心是三角形的几何中心,通常也称为重心,三角形的三条中线(顶点和对边的中点的连线)交点,此点即为重心。
三、什么是三角形的质心,角平分线分对边是1:2么
三角形三条中线的交点是三角形的重心或质心。三角形重心分中线的比是2:1
角平分线分对边之比等于夹这个角的三角形两边之比,具体数值要根据三角形两边来定。三条角平分线交点到三边距离相等,此交点分角平分线的比例没有固定关系。
四、三角形的中心是什么意思
通常是指型心,
面的形心就是截面图形的几何中心,质心是针对实物体而言的,而形心是针对抽象几何体而言的,对于密度均匀的实物体,质心和形心重合。
五、直角三角形质心怎么求
质心对平面三角形来说就是3条边中线的交点,这个交点是中线的3分点。
重心在写斜边上,且为斜边的中点,重心到71边的距离根据三角形相似原理,为另一边10的一半,即重心到71的这一边的距离是5。
均匀三角σ是一个单位面积的质量值,所以总质量M就是面积*σ,m就是横坐标x所在区域的质亮,即m=σ*y=σ*(a-x)*tan θ。这里利用积分的办法,将d(σ*(a-x)*tan θ)转化为dx,就得到以上解了。
直角三角形中,斜边上的中线等于斜边的一半(即直角三角形的外心位于斜边的中点,外接圆半径R=C/2)。该性质称为直角三角形斜边中线定理。
扩展资料:
1、直角三角形两直角边的平方和等于斜边的平方。如图,∠BAC=90°,则AB²+AC²=BC²(勾股定理)
2、在直角三角形中,两个锐角互余。如图,若∠BAC=90°,则∠B+∠C=90°
3、直角三角形中,斜边上的中线等于斜边的一半(即直角三角形的外心位于斜边的中点,外接圆半径R=C/2)。该性质称为直角三角形斜边中线定理。
4、直角三角形的两直角边的乘积等于斜边与斜边上高的乘积。
参考资料来源:百度百科-直角三角形
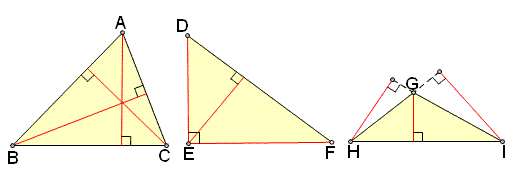
六、三角形重心,什么的,可以为我解答一下吗?还有他们的性质
重心:三角形各边中线的交点,也叫质心;
垂心:各边垂线的交点;
内心:角平分线的交点,也是内切圆的圆心;
外心:外接圆的圆心