一、什么是垂线四年级
垂线的定义是两条直线相交,并且有一个角是直角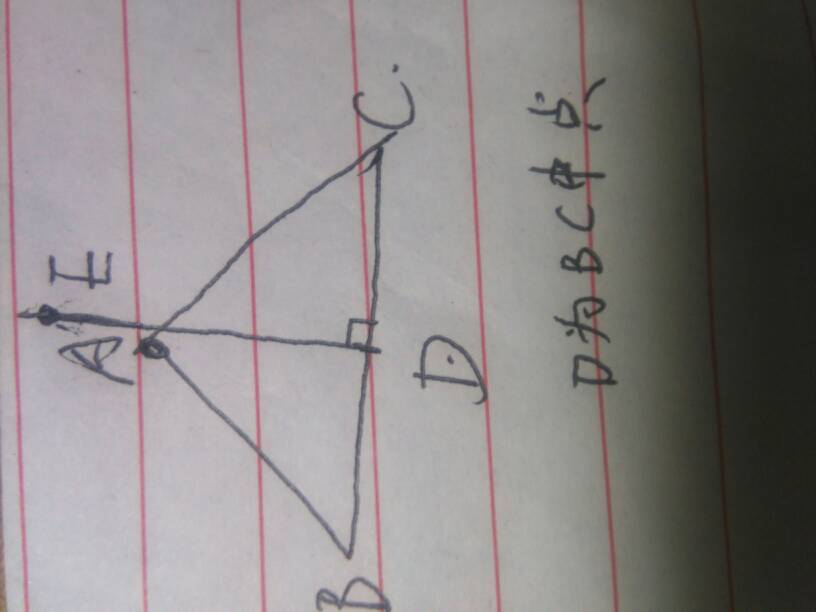
垂线也就是两条线互相垂直,那么一条直线就叫做另一条直线的垂线,而它们相交的这个点就被称之为垂足。当然如果这两条直线相交之后所形成的4个角都是直角,那么这两条直线也可以叫做互为垂线。
垂线的定理和性质
1、垂直公理:在同一平面内,过一点(直线上或直线外)有且只有一条直线与已知直线垂直。
2、垂线段公理:直线外一点与直线上各点连接的所有线段中,垂线段最短(简称“垂线段最短”)。
3、直线外一点到这条直线的垂线段的长度,叫做点到直线的距离。线段AB叫做点A到直线BC的垂线段,它的长度就是点A到直线BC的距离
二、垂线的定义是什么?
若两条直线相交,且相交后的四个角都为90°,则这两条直线互相垂直,即为互为垂线。
垂线的定义中,只是规定了两直线交角的大小(90°),并没有规定两条直线的位置如何。也就是说,不论一条直线的位置如何,只要另一条与它的交角是90°,其中任何一条直线就是另一条直线的垂线。
扩展资料
画垂线有两种情况,一种是已知一条直线,过这个直线之外的一个点画这个直线的垂线;另一种情况是已知一条直线,过这个线上的某一点作这个直线的垂线。
这两种情况画垂线都需要用到工具,有直尺、直角三角尺还有笔。
1、第一种情况,首先把直尺放好,直尺的一条边要和已知的那条直线重合,然后把直角三角尺的其中一个直角边靠在直尺上,保持三角尺的另一个边和直尺垂直的情况下,慢慢移动直角三角尺。
直到直线外的某一点和直尺三角尺的另一条边重合,最后沿着直角三角尺的另一条边过直线外的那一点画出来直线,这条直线就是那条已知直线的垂线。
2、第二种情况,也是要先把直尺作为一个标准放好,直尺的一条边要和已知的直线重合在一起,把直角三角形的一个直角边靠在直尺上,保持直尺不动。
直角三角尺慢慢移动,直到直角三角尺的顶点和已知的那个点重合,沿着直角三角尺的另一条直角边过已知的点画一条直线,这条直线就是要画的垂线。
参考资料来源:百度百科-垂线
三、什么叫做垂线
垂线的定义是两条直线相交,并且有一个角是直角,也就是两条线互相垂直,那么一条直线就叫做另一条直线的垂线,而它们相交的这个点就被称之为垂足。当然如果这两条直线相交之后所形成的4个角都是直角,那么这两条直线也可以叫做互为垂线,其垂线的基本特性就是过直线上或者直线外的一点,有并且只有一条直线跟已知的这条直线垂直,前提当然是要在同一个平面上。另外,从直线外的一点任意方向到这条直线所连接的所有线段之中,垂直线段都是最短的。
四、什么是垂线?
当两条直线相交所成的四个角中,有一个角是直角时,即两条直线互相垂直,其中一条直线叫做另一直线的垂线,交点叫垂足。
垂线段是一个图形,点到直线的距离是一个数量。
垂线的定义中,只是规定了两直线交角的大小(90°),并没有规定两条直线的位置如何。也就是说,不论一条直线的位置如何,只要另一条与它的交角是90°,其中任何一条直线就是另一条直线的垂线。
垂线的基本性质是:
(1)过直线上或直线外的一点,有且只有一条直线和已知直线垂直(在同一平面内)。
(2)从直线外一点到这条直线上各点所连的线段中,垂直线段最短。
五、垂线的定义、性质和判定是什么?
垂线的基本性质是:
(1)过直线上或直线外的一点,有且只有一条直线和已知直线垂直.
(2)从直线外一点到这条直线上各点所连的线段中,垂直线段最短.